Edge based analysis with edge values
The edge based analysis with network statistics can be conducted using the function sem.net.edge. The idea behind this method is that the edge values can be the unit of analysis if we transform non-network covariates into pair-based values.
Simulated Data Example
To begin with, a random simulated dataset can be used to demonstrate the usage of the node-based network statistics approach. The code below generate a simulated network net with four non-network covariates x1 - x4 which loads on two latent variables lv1, lv2.
set.seed(100)
nsamp = 100
net <- data.frame(ifelse(matrix(rnorm(nsamp^2), nsamp, nsamp) > 1, 1, 0))
mean(net) # density of simulated network
lv1 <- rnorm(nsamp)
lv2 <- rnorm(nsamp)
nonnet <- data.frame(x1 = lv1*0.5 + rnorm(nsamp),
x2 = lv1*0.8 + rnorm(nsamp),
x3 = lv2*0.5 + rnorm(nsamp),
x4 = lv2*0.8 + rnorm(nsamp))With the simulated data, we can define a model string with lavaan syntax that specifies the measurement model as well as the relationship between the network and the non-network variables. In this case, we are using net as a mediator between the two latent variables. Since data are generated randomly, the effects should be small overall.
model <-'
lv1 =~ x1 + x2
lv2 =~ x3 + x4
lv1 ~ net
lv2 ~ lv1
'Arguments passed to the sem.net.edge function includes the model and the dataset. Note that data here should be a list with two elements, one being the named list of all network variables and one being the dataframe containing non-network variables. A summary function can be used to look at the output, and the function path.networksem can be used to look at mediation effects.
data = list(network = list(net = net), nonnetwork = nonnet)
set.seed(100)
res <- sem.net.edge(model = model, data = data, type = 'difference')
summary(res)
path.networksem(res, "net", "lv1", "lv2")The output is shown below.
> summary(res)
The SEM output:
lavaan 0.6.15 ended normally after 58 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 10
Number of observations 10000
Model Test User Model:
Test statistic 1.584
Degrees of freedom 4
P-value (Chi-square) 0.812
Model Test Baseline Model:
Test statistic 2296.506
Degrees of freedom 10
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.003
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -75480.300
Loglikelihood unrestricted model (H1) -75479.508
Akaike (AIC) 150980.601
Bayesian (BIC) 151052.704
Sample-size adjusted Bayesian (SABIC) 151020.925
Root Mean Square Error of Approximation:
RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.009
P-value H_0: RMSEA <= 0.050 1.000
P-value H_0: RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.003
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
lv1 =~
x1 1.000
x2 0.810 0.063 12.894 0.000
lv2 =~
x3 1.000
x4 0.302 0.056 5.377 0.000
Regressions:
Estimate Std.Err z-value P(>|z|)
lv1 ~
net 0.053 0.039 1.371 0.170
lv2 ~
lv1 -0.482 0.035 -13.683 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.x1 1.964 0.076 25.814 0.000
.x2 2.104 0.055 38.145 0.000
.x3 -0.681 0.527 -1.293 0.196
.x4 2.865 0.063 45.557 0.000
.lv1 0.898 0.077 11.708 0.000
.lv2 2.678 0.529 5.061 0.000
> path.networksem(res, "net", "lv1", "lv2")
predictor mediator outcome apath bpath indirect
1 net lv1 lv2 0.05287153 -0.4823857 -0.02550447
indirect_se indirect_z
1 0.01705778 -1.495181Empirical Data Example
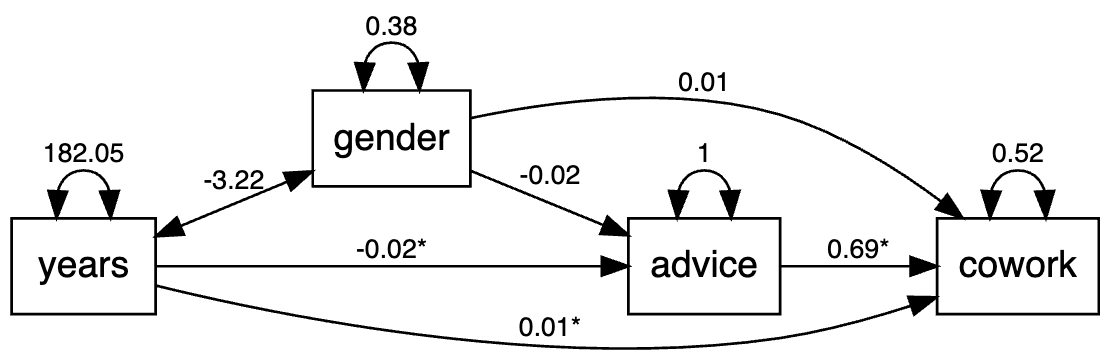
As an empirical example, we analyze the the attorney cowork and advice networks. In this example, the advice network is predicted by gender and years in practice, and the cowork network is predicted by the advice network, gender, and years in practice all together. In this case, the advice network acts as a mediator, while gender and years in practice exert indirect effect onto the cowork network through the advice network in addition to having direct effects. The model specification is given below.
non_network <- read.table("data/attorney/ELattr.dat")[,c(3,5)]
colnames(non_network) <- c('gender', 'years')
non_network$gender <- non_network$gender - 1
network <- list()
network$advice <- read.table("data/attorney/ELadv.dat")
network$cowork <- read.table("data/attorney/ELwork.dat")
model <-'
advice ~ gender + years
cowork ~ advice + gender + years
'
To use the function sem.net.edge(), we need to specify whether the covariate values to be run with the social network edge values in SEM should be calculated as the ”difference” across two individuals or the ”average” across two individuals. Here, the argument ordered = c("cowork", "advice") is used to tell lavaan that the outcome variables cowork and advice are binary.
set.seed(100)
res <- sem.net.edge(model = model, data = data,
network = network, type = "difference", ordered = c("cowork", "advice")) This model is again estimated in two stages. In the first stage, the non-network variables of gender and years in practice are converted to be pairwise such that years in practice for the pair of individuals $i$ and $j$ would be the difference between years inpractice for individual $i$ and for individual $j$. After obtaining the pairwise non-network statistics, these variables are compiled into the same file as the network edge variables, which are binary, and also pairwise. This data frame is then given to lavaan to be used with the SEM framework. Thus, in this model, SEM used each pair of individuals as the unit of analysis. The output can be access via summary(res$estimates, fit=TRUE) and is shown as below.
lavaan 0.6.15 ended normally after 19 iterations
Estimator DWLS
Optimization method NLMINB
Number of model parameters 7
Number of observations 5041
Model Test User Model:
Standard Scaled
Test Statistic 0.000 0.000
Degrees of freedom 0 0
Model Test Baseline Model:
Test statistic 1343.292 1343.292
Degrees of freedom 1 1
P-value 0.000 0.000
Scaling correction factor 1.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000 1.000
Tucker-Lewis Index (TLI) 1.000 1.000
Robust Comparative Fit Index (CFI) NA
Robust Tucker-Lewis Index (TLI) NA
Root Mean Square Error of Approximation:
RMSEA 0.000 0.000
90 Percent confidence interval - lower 0.000 0.000
90 Percent confidence interval - upper 0.000 0.000
P-value H_0: RMSEA <= 0.050 NA NA
P-value H_0: RMSEA >= 0.080 NA NA
Robust RMSEA NA
90 Percent confidence interval - lower NA
90 Percent confidence interval - upper NA
P-value H_0: Robust RMSEA <= 0.050 NA
P-value H_0: Robust RMSEA >= 0.080 NA
Standardized Root Mean Square Residual:
SRMR 0.000 0.000
Parameter Estimates:
Standard errors Robust.sem
Information Expected
Information saturated (h1) model Unstructured
Regressions:
Estimate Std.Err z-value P(>|z|)
advice ~
gender -0.019 0.040 -0.463 0.643
years -0.018 0.002 -9.354 0.000
cowork ~
advice 0.691 0.019 36.651 0.000
gender 0.013 0.040 0.323 0.747
years 0.013 0.002 7.248 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
.advice 0.000
.cowork 0.000
Thresholds:
Estimate Std.Err z-value P(>|z|)
advice|t1 0.956 0.022 43.812 0.000
cowork|t1 1.037 0.022 48.049 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.advice 1.000
.cowork 0.523
Scales y*:
Estimate Std.Err z-value P(>|z|)
advice 1.000
cowork 1.000The indirect effects can be calculated as below.
> path.networksem(res, "gender", "advice", "cowork")
predictor mediator outcome apath bpath indirect
1 gender advice cowork -0.01856161 0.6909742 -0.01282559
indirect_se indirect_z
1 0.01304666 -0.9830558